[자료구조] 7일차 트리의 활용

정렬된 상태를 유지하는 배열의 시간 복잡도

📌 임의의 자료들을 담고 있는 자료구조 A가 있다고 가정할 때, A는 항상 정렬된 상태를 유지해야 한다.
만약 A가 배열이라면 자료의 추가, 삭제, 탐색은 다음과 같다.

 

• 정렬된 상태를 유지하는 배열의 추가와 삭제 연산은 O(n)의 시간 복잡도를 가진다.
• 이진 탐색을 이용하면 정렬된 배열 내에서으 자료 탐색을 o(logn)만에 수행할 수 있다.

 

📌 이진 탐색

• 정렬된 배열의 중간값과 찾는 값의 크기를 비교하고 중간값보다 작은 경우에는 중간값을 기준으로 좌측, 중간값보다 큰 경우에는 우측을 대상으로 다시 탐색

ex) 상대방이 생각하고 있는 숫자 맞추기(업 다운 게임)

: o(log100) = 6.64…이므로 숫자 맞히기까지 걸리는 횟수로 최악의 경우 7회임

 

📌 이진 탐색 트리

• 항상 정렬된 상태를 유지하는 자료구조
• 왼쪽 서브트리는 그 정점보다 같거나 작은 정점들로만, 오른쪽 서브 트리는 그 정점의 값보다 큰 정점들로만 이루어져 있음.

 

0 추가하기

: 루트노드부터 0이랑 비교해서 작은 수이기 때문에 계속 왼쪽으로 가게 됨.

 

 

5 삭제하기

1. 4 < 5 : 오른쪽으로 감
2. 6 > 5 : 왼쪽으로 감.
3. 5 찾아서 삭제

 

만약 중간에 있는 정점을 삭제해야 한다면?

• 6의 오른쪽 서브 트리 중 가장 왼쪽에 있는 정점인 7이 6의 위치를 대신함.

 

 

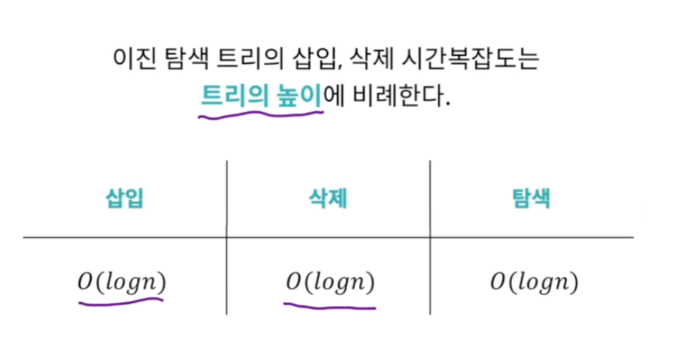
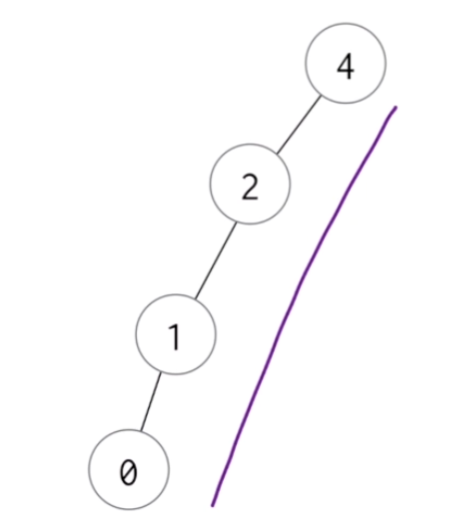
📌 이진 트리의 문제점 (편향 이진 트리)

한쪽으로 편향된 이진 탐색 트리가 존재 가능함. 이진 탐색 트리의 장점을 살리지 못함. 실제로 많이 활용되는 이진 탐색 트리는 자가 균형 이진 탐색 트리라고 불리는 “레드 블랙 트리” 사용